文字
背景
行間
2018年6月の記事一覧
閑話 黄金比 その１
sakura-h
先日、参加した千葉県高等学校教育研究会数学部会の春季研究大会の講演で、講師の先生が和算の問題を現在使える公式を使わずに解くとしたらというお話しのなかで「黄金比」を使って解くというものがあり、そういえば「黄金比」自体とっても興味深いものであることを思い出し、今回はその一端に触れてみたい。
黄金比は、エウクレイデス（ユークリッド）が「原論」で明快な定義を与えている。そこでは線分を単純に分けて得られる線分の長さの比で次のように定義し「外中比」（黄金比のこと）と呼んでいる。
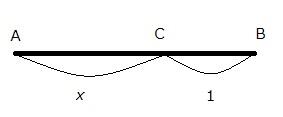「線分全体と長い切片との比が、長い切片と短い切片との比になる場合、線分は外中比に切り分けられたという。」左図でいえば、
が成り立っているということ。つまり、短い切片CBの長さを基準にして、$$AB=x,CB=1$$ とおくと $$\frac{x+1}{x}=\frac{x}{1}$$ が成り立つ。よって、両辺に$$x$$を掛けて整理すると、$$x^2-x-1=0$$ ・・・① が得られる。
問２ 問１で求めた正の解をΦ（ファイ）とする。Φの値はどのくらいだろう。
黄金比は、エウクレイデス（ユークリッド）が「原論」で明快な定義を与えている。そこでは線分を単純に分けて得られる線分の長さの比で次のように定義し「外中比」（黄金比のこと）と呼んでいる。
「線分全体と長い切片との比が、長い切片と短い切片との比になる場合、線分は外中比に切り分けられたという。」左図でいえば、問１ $$x$$の2次方程式①を解いてみよう。
問２ 問１で求めた正の解をΦ（ファイ）とする。Φの値はどのくらいだろう。
関数電卓等で近似値を確かめてみよう。
問３ 問２でΦの近似値を関数電卓等でΦ２ や $$\frac{1}{\phi}$$ の近似値を確かめてみよう。
何か、気づいたことはありますか。
問４ ΦとΦ２ 、 $$\frac{1}{\phi}$$ との関係を考えてみよう。
問５ 下の数式の値はいくつでしょう。
$$\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots } } } }$$
以上、興味をもった生徒は校長室まで話に来てください。
次回は 黄金比の連分数表現について
$$1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}$$
問３ 問２でΦの近似値を関数電卓等でΦ２ や $$\frac{1}{\phi}$$ の近似値を確かめてみよう。
何か、気づいたことはありますか。
問４ ΦとΦ２ 、 $$\frac{1}{\phi}$$ との関係を考えてみよう。
問５ 下の数式の値はいくつでしょう。
$$\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots } } } }$$
以上、興味をもった生徒は校長室まで話に来てください。
次回は 黄金比の連分数表現について
$$1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\cdots}$$